Проекция вектора на ось – одна из важных операций в линейной алгебре. Когда мы говорим о проекции вектора, мы имеем в виду его "отражение" на определенную ось или направление. Это позволяет нам разбить вектор на две составляющие: параллельную оси и ортогональную ей. В данной статье мы рассмотрим условие ортогональности проекции вектора на ось и почему результат может быть нулевым.
Условие ортогональности проекции вектора на ось заключается в том, что проекция вектора должна быть перпендикулярна оси, на которую он проецируется. Другими словами, вектор должен быть "выровнен" с осью, на которую его проецируют. Это достигается путем определения оператора проекции, который проецирует вектор на определенную ось и обеспечивает условие ортогональности.
Однако существует случай, когда результат проекции вектора на ось может быть нулевым. Это происходит, когда вектор направлен параллельно оси, на которую его проецируют. В этом случае проекция вектора на ось будет иметь нулевую длину и будет считаться нулевым вектором. Это можно представить себе как отсутствие компоненты вектора в направлении выбранной оси.
Что такое проекция вектора на ось?

Проекция вектора на ось может быть положительной или отрицательной величиной, в зависимости от направления вектора и оси. Если направление вектора совпадает с направлением положительной оси, проекция будет положительной. Если направление вектора противоположно направлению положительной оси, проекция будет отрицательной.
Ортогональность и нулевой результат проекции вектора на ось связаны между собой. Если проекция вектора на ось равна нулю, это значит, что вектор ортогонален этой оси, то есть, перпендикулярен ей. Если проекция вектора на ось не равна нулю, это значит, что вектор не ортогонален этой оси и имеет некоторую компоненту, направленную вдоль этой оси.
Проекция вектора на ось является важным инструментом в геометрии и физике, позволяющим разбить вектор на компоненты и анализировать его свойства вдоль определенного направления.
Основные понятия проекции вектора на ось

Для того чтобы найти проекцию вектора на ось, необходимо найти длину этой проекции и ее направление. Длина проекции равна произведению длины вектора на косинус угла между вектором и осью. Направление проекции всегда сонаправлено с выбранной осью.
Проекция вектора на ось может быть положительной или отрицательной, в зависимости от угла между осью и вектором. Если угол между осью и вектором составляет менее 90 градусов, проекция будет положительной. Если же угол превышает 90 градусов, проекция будет отрицательной.
Очень важно отметить, что если проекция вектора на ось равна нулю, это означает, что вектор ортогонален данной оси. Другими словами, вектор не имеет составляющих вдоль этой оси.
Проекция вектора на ось может быть использована в различных областях науки и техники, например, в физике, где она позволяет находить составляющие силы по определенным направлениям. Она также применяется в компьютерной графике, где проекции векторов используются для создания эффекта трехмерности.
Геометрическое изображение проекции вектора на ось
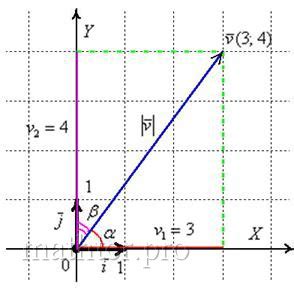
Геометрическое изображение проекции вектора на ось можно представить следующим образом:
- Начните с вектора, который нужно проецировать.
- Проведите перпендикуляр от начала этого вектора к оси, на которую нужно его проецировать.
- Точка пересечения перпендикуляра с осью является концом проекции вектора.
Таким образом, проекция вектора на ось представляет собой линию, которая соединяет начало вектора с точкой пересечения перпендикуляра с осью.
Значение проекции вектора на ось может быть отрицательным или положительным, в зависимости от направления вектора от начала до конца. Если вектор направлен в противоположную сторону оси, проекция будет отрицательной, в противном случае она будет положительной.
Важно отметить, что если ось является ортогональной, то проекция будет равна нулю. Это означает, что вектор полностью ортогонален данной оси и не имеет проекции на нее.
Геометрическое изображение проекции вектора на ось является важным концептом в линейной алгебре, используется во многих областях математики и физики, а также имеет практическое применение в графическом моделировании и компьютерной графике.
Формулы для вычисления проекции вектора на ось

Если ось задана вектором единичной длины a, а вектор для проекции задан вектором v, то проекция вектора на ось вычисляется по формуле:
proja(v) = (v · a) * a
где v · a представляет скалярное произведение векторов v и a.
Если ось задана координатным направлением, то для вычисления проекции вектора на ось использование следующих формул:
- Если ось задана координатным направлением x, проекция вектора v на ось вычисляется по формуле: projx(v) = (vx, 0, 0)
- Если ось задана координатным направлением y, проекция вектора v на ось вычисляется по формуле: projy(v) = (0, vy, 0)
- Если ось задана координатным направлением z, проекция вектора v на ось вычисляется по формуле: projz(v) = (0, 0, vz)
Проекция вектора на ось позволяет определить векторную составляющую вектора, расположенную вдоль оси, игнорируя компоненты, ортогональные этой оси. Это понятие является важным инструментом в различных областях, таких как физика, геометрия и компьютерная графика.
Условие ортогональности проекции вектора на ось

Условие ортогональности проекции вектора на ось заключается в том, что вектор проекции должен быть перпендикулярен оси, на которую он проецируется. Или, другими словами, скалярное произведение вектора проекции и вектора оси должно быть равно нулю:
| Вектор проекции: | P |
| Вектор оси: | A |
Условие ортогональности можно записать в виде уравнения:
P ⋅ A = 0
Если данная формула выполняется, это означает, что проекция вектора ортогональна оси и имеет нулевую длину. Если соотношение не выполняется, значит, вектор не попадает на ось и его проекция будет отличной от нуля.
Условие ортогональности проекции вектора на ось является одним из основных свойств проекции и широко используется в различных областях, включая физику, математику и компьютерную графику.
Взаимосвязь проекции вектора на ось и ортогональности
Для начала, нужно разобраться, что такое ортогональность. Ортогональные векторы - это такие векторы, у которых скалярное произведение равно нулю. Иными словами, они перпендикулярны друг другу.
Теперь вернемся к проекции вектора на ось. Если вектор проецируется на ось, то результат этой проекции будет вектором, лежащим на этой оси. И что это значит? Это значит, что вектор направлен вдоль оси. А какой вектор может быть перпендикулярен оси? Только нулевой вектор, так как он не имеет направления.
Таким образом, если проекция вектора на ось равна нулевому вектору, то это означает, что вектор ортогонален этой оси. В противном случае, вектор направлен вдоль этой оси и не ортогонален ей.
Итак, мы видим взаимосвязь между проекцией вектора на ось и ортогональностью. Проекция вектора на ось будет нулевым вектором тогда и только тогда, когда данный вектор ортогонален этой оси.
Когда результат проекции вектора на ось является нулевым?

Это может быть полезным в различных ситуациях. Например, если мы хотим определить, в какой мере вектор сонаправлен или противонаправлен оси. Если результат проекции равен нулю, то это может означать, что вектор и ось имеют противоположные направления.
Также, если результат проекции вектора на ось является нулевым, это может дать нам информацию о специфической свойстве вектора или оси. Например, если вектор представляет собой силу, а ось - поверхность, то нулевой результат проекции может указывать на отсутствие работы, совершаемой силой на данной поверхности.
Примеры применения проекции вектора на ось в практике

1. Физика:
В физике проекция вектора на ось используется для решения различных задач. Например, при расчете силы, действующей на тело по наклонной плоскости, необходимо найти проекцию веса этого тела на ось, параллельную плоскости. Также проекция вектора используется для нахождения проекции скорости тела на ось.
2. Графика и компьютерные игры:
В компьютерной графике и играх часто приходится работать с векторами. Например, при построении трехмерной сцены необходимо проецировать векторы направления света на оси экрана для определения освещения пикселей. Также проекция вектора применяется для определения видимости объектов и для расчета столкновений в играх.
3. Биология:
В биологии проекция вектора на ось может использоваться для анализа направления движения животных. Например, при изучении миграции птиц проекция вектора их перемещения на ось времени может помочь в определении маршрутов и скорости миграции.
4. Финансы и экономика:
В финансовой аналитике и экономических расчетах проекция вектора на ось может использоваться для анализа временных рядов и предсказания трендов. Например, при анализе фондового рынка можно проецировать вектор доходности актива на ось времени для оценки его производительности и определения возможных будущих изменений.
Все эти примеры демонстрируют широкий спектр практических применений проекции вектора на ось. Найдя проекцию вектора на определенную ось, мы можем получить ценную информацию о его характеристиках или использовать ее для решения различных задач и анализа данных.



