В наше современное информационное общество мы привыкли опираться на технологии и инструменты, которые помогают нам выполнить самые разнообразные задачи, включая расчеты и вычисления. Однако, возникают ситуации, когда доступ к калькулятору отсутствует или желание проверить свои математические навыки без его использования. Как же найти значение сложного выражения без калькулятора? В этой статье мы рассмотрим несколько методов, которые помогут вам справиться с этой задачей.
Первый метод, который мы рекомендуем попробовать, основан на использовании известных математических законов и правил. Это позволит сократить выражение и упростить его подсчет. Например, если у вас есть выражение вида (2 + 3) * 4, то сначала можно выполнить операцию в скобках (2 + 3 = 5), а затем умножить полученное значение на 4 (5 * 4 = 20). Таким образом, вы сможете найти значение выражения без использования калькулятора.
Второй метод предлагает использовать метод пристального взгляда (метод "глазомера"). Он подразумевает оценку приближенного значения выражения на основе предварительной оценки каждой операции и приближенного значения чисел. Например, если у вас есть выражение 37 * 24, вы можете оценить это как примерно 40 * 20 = 800. Это приближенное значение даст вам представление о том, чего ожидать, и поможет вам справиться без калькулятора.
Наконец, стоит отметить, что найти значение выражения без калькулятора может быть сложно, особенно если оно содержит сложные операции и большие числа. Однако, с практикой и знанием математических правил, вы сможете развить свои навыки расчета и выполнить вычисления без помощи калькулятора. Попробуйте использовать эти методы и улучшите свои математические навыки уже сегодня!
Основные способы нахождения значения выражения без калькулятора

Определение значения математических выражений без использования калькулятора может быть полезным навыком в различных ситуациях. Ниже представлены несколько основных способов решения таких задач:
| Способ | Описание |
|---|---|
| Арифметические свойства | Используйте арифметические свойства для упрощения и преобразования выражения. Например, можно применить дистрибутивное свойство, факторизацию или сокращение дроби. |
| Приближенные значения | Если точное значение не требуется, можно использовать приближенное вычисление. Например, можно округлить значения чисел или использовать числа с ограниченным количеством значащих цифр. |
| Использование таблицы значений | Заполните таблицу значений, подставляя различные значения переменных в выражение, и оцените результат. Таким образом, вы сможете приближенно определить значение выражения. |
| Использование функций | Если в выражении присутствуют функции, вы можете использовать значение функций в таблице значений или знания о значениях функций в особых случаях. |
| Геометрические методы | В некоторых случаях можно использовать геометрические методы для приближенного определения значения выражений. Например, можно построить график функции и оценить значение по виду графика или использовать знание геометрических фигур для аппроксимации значения выражения. |
Определение значения выражений без калькулятора требует некоторого уровня математического понимания и навыков, поэтому часто требуется практика и опыт для достижения точных результатов. Однако, использование вышеуказанных способов может помочь вам справиться с задачами без использования калькулятора.
Использование математических основных операций

Математические основные операции включают в себя сложение (+), вычитание (-), умножение (*) и деление (/). Использование этих операций позволяет найти значение выражения без необходимости использования калькулятора.
Например, для нахождения значения выражения 2 + 3, нужно сложить числа 2 и 3, что даст результат 5.
Если необходимо найти разность двух чисел, можно использовать операцию вычитания. Например, для нахождения значения выражения 8 - 5, нужно вычесть число 5 из числа 8, что даст результат 3.
Умножение позволяет находить произведение двух чисел. Например, чтобы найти значение выражения 4 * 6, нужно умножить число 4 на число 6, что даст результат 24.
Если требуется найти частное двух чисел, используется операция деления. Например, для нахождения значения выражения 15 / 3, нужно разделить число 15 на число 3, что даст результат 5.
Если в выражении присутствуют несколько операций, нужно сначала выполнить операции умножения и деления, а затем сложение и вычитание. Приоритетность операций можно изменить с помощью скобок.
Например, для нахождения значения выражения 2 + 3 * 4, нужно сначала выполнить умножение: 3 * 4 = 12, а затем сложение: 2 + 12 = 14.
Таким образом, использование математических основных операций позволяет легко и быстро находить значение выражений без использования калькулятора.
Алгебраические методы подсчета выражений

Подсчет выражений без калькулятора может быть выполнен с использованием алгебраических методов. Эти методы позволяют упростить выражение и найти его значение с помощью алгебраических правил и свойств чисел.
Один из таких методов - использование свойств операций. Например, для выражения вида (а + б) * с можно применить свойство дистрибутивности операции умножения относительно сложения: (а + б) * с = а * с + б * с. Таким образом, можно разбить выражение на несколько более простых и подсчитать их значения по отдельности.
Другой метод - использование алгебраических правил сокращенного умножения, деления и возведения в степень. Например, для выражения а^2 - b^2 можно применить формулу разности квадратов: а^2 - b^2 = (а - b) * (а + b). Таким образом, можно преобразовать выражение и подсчитать его значение с помощью алгебраических операций.
Для сложных выражений можно использовать метод замены переменных. Замена переменных позволяет привести выражение к более простому виду, в котором его значение будет легче вычислить. К примеру, если в выражении присутствует подвыражение, которое можно заменить на новую переменную, то можно провести замену и получить новое, более простое выражение.
Также можно использовать обратные операции для упрощения выражений. Например, если в выражении присутствует сложение, можно применить обратную операцию вычитания для упрощения выражения.
Таким образом, алгебраические методы позволяют подсчитывать сложные выражения без калькулятора, основываясь на свойствах операций, алгебраических правилах и замене переменных.
Наглядное представление выражений и использование геометрических фигур

Когда речь идет о нахождении значения выражения без калькулятора, использование геометрических фигур может быть полезным. Это позволяет наглядно представить выражение и визуализировать его значение.
Один из способов использования геометрических фигур - использование диаграммы. Вы можете нарисовать диаграмму, на которой каждая фигура представляет часть выражения. Например, если у вас есть выражение 2 + 3, вы можете нарисовать две фигуры, представляющие числа 2 и 3, и сложить их вместе, чтобы получить значение выражения.
Еще один способ использования геометрических фигур - использование моделей. Например, если у вас есть выражение 4 x 5, вы можете использовать модель, представляющую 4 группы из 5 объектов каждая. Затем вы можете посчитать общее количество объектов в модели, чтобы получить значение выражения.
Использование геометрических фигур позволяет визуально представить выражение и выполнить вычисления без использования калькулятора. Это особенно полезно для учащихся, которым сложно представить абстрактные математические концепции. Такой подход также помогает воспринимать математику более интересно и запоминающимся способом.
Применение логических и булевых операций
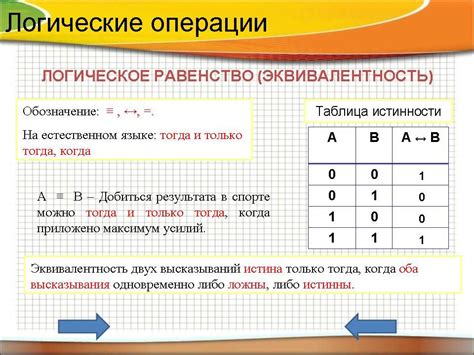
При решении математических задач без калькулятора можно применять логические и булевые операции. Эти операции позволяют комбинировать и анализировать различные значения и условия, что упрощает и ускоряет процесс вычислений.
Логические операции включают в себя операции сравнения, такие как равно (==), не равно (!=), больше (>), меньше (<), больше или равно (>=), меньше или равно (<=). При использовании этих операций получаем результат в виде логического значения - истина (true) или ложь (false).
Булевы операции включают в себя операции логического И (&&), логического ИЛИ (



