Определение количества градусов угла является важной задачей в геометрии и физике. Градусы используются для измерения размеров углов и они позволяют нам точно определить их величину. Но как именно узнать, сколько градусов составляет данный угол?
Существует несколько способов определения количества градусов угла. Один из самых простых - это использование угломера, который является особой инструментом для измерения углов. Этот инструмент позволяет легко и точно измерить количество градусов, составляющих данный угол.
Если у вас нет угломера под рукой, вы можете воспользоваться математическим методом. В геометрии существует формула, которая позволяет рассчитать количество градусов угла. Для этого необходимо знать длины сторон треугольника, составленного по данному углу, и использовать тригонометрический закон синусов или косинусов.
Итак, измерение градусов угла - это важный навык, который может быть полезен в различных сферах жизни. Будь то учеба, работа или повседневные задачи, знание этого навыка поможет вам решать разнообразные задачи и задания, требующие определения углов.
Что такое угол?

Углы измеряются в градусах (°). Полный круг делится на 360 градусов, причем каждый градус равен 1/360 от полного круга. Угол, равный 90 градусам, называется прямым углом. Угол, меньший 90 градусов, называется остроугольным углом, а угол, больший 90 градусов, называется тупоугольным углом.
Важно:
- Соседние углы – углы, общей вершиной которых является одна точка, а лучи образуют продолжение друг друга.
- Вертикальные углы – углы, имеющие общую вершину, а лучи являются противоположными сторонами.
- Сумма всех углов треугольника равна 180 градусам.
Изучение углов помогает в решении различных задач и построении геометрических фигур. Зная количество градусов угла, мы можем определить его тип и выполнять дальнейшие вычисления с углами.
Способы измерения угла

Существует ряд способов измерения угла:
- Градусная мера угла – самый распространенный способ измерения углов. Градусная мера основана на делении полного круга на 360 равных частей. Таким образом, прямой угол равен 90 градусам, а полный круг – 360 градусов.
- Радианная мера угла – используется в математике и физике. Радиан – это длина дуги окружности, равная радиусу этой окружности. В этой мере прямой угол равен половине радиуса окружности.
- Грады – это еще одна система измерения углов, часто используемая в геодезии и картографии. Град делит полный круг на 400 равных частей, поэтому прямой угол равен 100 градам.
Кроме того, существует множество инструментов для измерения углов, таких как транспортиры, гониометры, угломеры и прочие. С их помощью можно точно и быстро измерять углы в различных областях науки и техники.
Независимо от выбранного способа измерения, углы играют важную роль в геометрии, физике, инженерии и других научных дисциплинах, где требуется изучение пространственных отношений и измерение направлений.
Градусная мера
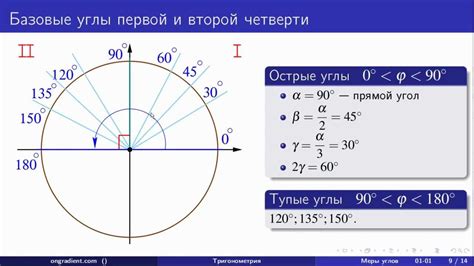
Градусная мера применяется для измерения различных видов углов, таких как прямой угол (90°), прямой угол (180°) и окружностные углы (360°).
Для определения градусной меры угла используется инструмент под названием градусник. Градусник представляет собой полукруглую шкалу, разделенную на 180 равных частей. Первая половина (от 0° до 90°) представляет углы меньше прямого угла, вторая половина (от 90° до 180°) - углы больше прямого угла.
Для измерения угла с помощью градусника следует поместить его так, чтобы ось градусника проходила через вершину угла, а ноль градусов на шкале градусника направлен вдоль одной из сторон угла. Затем считывается значение угла, которое отображается на шкале градусника.
Градусная мера также благополучно сочетается с другими системами измерения углов, такими как радианы и грады. Для перевода углов из градусов в радианы и наоборот существуют специальные математические формулы и коэффициенты.
Важно помнить, что градусная мера является одной из наиболее распространенных и удобных систем измерения углов, которая применяется во многих областях науки и техники.
Радианная мера
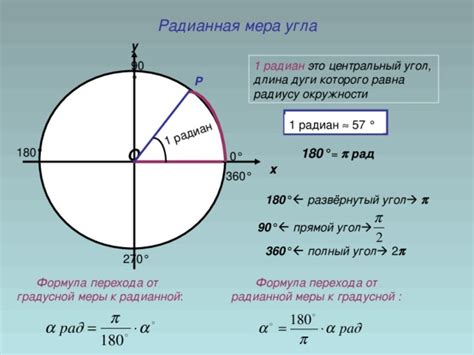
Обозначение радианной меры обычно состоит из числа, сопровождаемого символом "радиан". Например, π радиан, 2π радиан и т.д.
Переход от градусной меры к радианной мере осуществляется по формуле: радианная мера = градусная мера * (π/180). Также можно использовать соотношение, что 180 градусов равны π радианам.
Радианная мера имеет много преимуществ при решении задач, связанных с геометрией и тригонометрией. Она позволяет легче и более точно выражать углы и их отношения в рамках различных формул и уравнений.
Для определения количества градусов угла по радианной мере используется обратное соотношение: градусная мера = радианная мера * (180/π).
Измерение с помощью транспортира
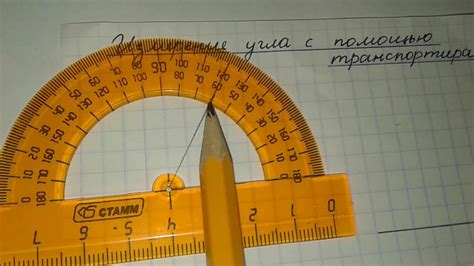
Для измерения угла с помощью транспортира:
- Поместите центр транспортира в точку, где угол начинается.
- Подвиньте транспортир, чтобы одна из линий лимба проходила через одну из сторон угла.
- Прочтите значение градусов на шкале транспортира, где проходит другая линия лимба. Это будет количество градусов угла.
Важно убедиться, что линия лимба проходит через точку начала угла и одну из его сторон. Также стоит помнить, что шкала транспортира часто имеет деления не только по градусам, но и по минутам и секундам.
Если у вас нет транспортира под рукой, можно сделать временный из бумаги, следуя инструкциям производителя. Или вы можете приобрести транспортир в школьной или художественной товарах, а также в интернет-магазинах.
Пользуйтесь транспортиром, чтобы визуально определить градусы угла и улучшить свои навыки измерения. И помните, практика делает мастера!
Измерение с помощью геометрических формул

Формула для вычисления величины угла в треугольнике основана на соотношении между длинами его сторон. В общем случае, если известны длины двух сторон треугольника и величина между ними угла, можно использовать формулу:
- Угол A = arccos((b^2 + c^2 - a^2)/(2bc))
- Угол B = arccos((c^2 + a^2 - b^2)/(2ac))
- Угол C = arccos((a^2 + b^2 - c^2)/(2ab))
Где a, b и c - длины сторон треугольника, а arccos - обратная функция косинуса.
Кроме того, для определения количества градусов угла можно использовать и другие геометрические формулы, такие как формула для вычисления площади треугольника или формула для вычисления длины дуги окружности. Важно понимать, что выбор формулы зависит от конкретной ситуации и известных данных.
Итак, для измерения количества градусов угла можно использовать различные геометрические формулы, которые основываются на соотношениях между длинами сторон, площадью или длиной дуги. Зная эти формулы и имея соответствующие данные, можно точно определить величину угла в градусах.
Измерение с помощью специализированных инструментов

Угломер представляет собой специальное устройство, оснащенное шкалой с делениями, которые представляют собой градусы. Чтобы измерить угол с помощью угломера, необходимо поместить его на вершину угла так, чтобы линия деления совпадала с осью угла.
Еще одним инструментом, который используется для измерения углов, является гониометр. Гониометр состоит из фиксированной и подвижной линий, которые позволяют определить угол между ними. Для измерения угла с помощью гониометра необходимо поместить его на вершину угла так, чтобы вершина линий совпадала с вершиной угла.
Еще одним распространенным инструментом для измерения углов является универсальный измерительный инструмент или скоб-шаблон. Данный инструмент представляет собой металлическую полоску с различными делениями и отверстиями, которые позволяют измерять углы различной формы.
| Название инструмента | Описание |
|---|---|
| Угломер | Оснащен шкалой с делениями, используется для измерения точного угла. |
| Гониометр | Состоит из фиксированной и подвижной линий, позволяет определить угол между ними. |
| Универсальный измерительный инструмент | Металлическая полоска с различными делениями и отверстиями, позволяет измерять углы различной формы. |
Каждый из этих инструментов имеет свои особенности и применяется в зависимости от требований и условий измерения. Правильное использование специализированных инструментов позволяет получить наиболее точные результаты измерения углов.
Почему важно знать количество градусов угла

Геометрия и математика: Геометрические фигуры и их свойства определяются углами, которые составляют. Знание количества градусов в угле позволяет точно определить его тип и свойства. Оперирование углами также широко используется в алгебре и тригонометрии, что делает знание градусов углов неотъемлемой частью математической основы.
Строительство и архитектура: В этих отраслях знание углов является ключевым для правильного расчета и построения конструкций. Углы определяют направление стен, перекрытий и других элементов строения, а также форму различных архитектурных деталей. Ошибки в определении градусов углов могут привести к серьезным проблемам и выходу из строя конструкций.
География и навигация: В географии и навигации знание углов помогает определить направление движения, расстояние и местоположение объекта. Например, знание угла наклона земли позволяет определить широту и долготу точки на поверхности планеты.
Физика: В физике углы используются для измерения различных параметров, таких как скорость, ускорение, сила и траектория движения. Они также играют важную роль в оптике, механике и электродинамике.
Проектирование и производство: В промышленности и дизайне знание углов позволяет оптимизировать процессы проектирования и производства. Например, при проектировании обтекателей в автомобилестроении или формы для литья в металлургии.
В итоге, знание количества градусов угла играет важную роль в ряде различных дисциплин и практических задачах. Без него было бы значительно сложнее разрабатывать эффективные решения и обеспечивать точность в различных областях деятельности.



