Определение принадлежности точки многоугольнику является важной задачей в компьютерной геометрии. В различных приложениях, таких как графический редактор, система навигации или робототехника, необходимо точно определить, находится ли точка внутри многоугольника или снаружи.
Существует несколько методов решения этой задачи, однако некоторые из них не обеспечивают необходимую точность или требуют большого количества вычислений. В данной статье будет рассмотрен эффективный метод, основанный на алгоритме равенства количества пересечений прямых.
Основная идея метода заключается в следующем: для определения принадлежности точки многоугольнику, проводятся лучи из этой точки во все направления. Затем подсчитывается количество пересечений этих лучей с гранями многоугольника. Если количество пересечений четное, то точка находится снаружи многоугольника, а если нечетное - внутри. Этот метод называется "методом четности пересечений".
Описанный метод является достаточно эффективным и работает для любого выпуклого или невыпуклого многоугольника. Он позволяет определить принадлежность многоугольнику за линейное время, то есть время выполнения алгоритма не зависит от числа граней многоугольника. Более того, этот метод может быть легко реализован в программе, используя основные операции алгебры и геометрии.
Метод определения принадлежности точки многоугольнику
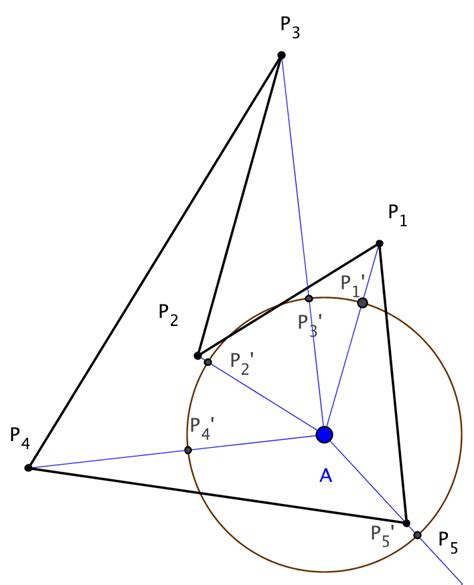
Существует несколько методов определения принадлежности точки многоугольнику, однако, в данной статье рассмотрим эффективный метод на основе равенства суммы углов.
Алгоритм действует следующим образом:
- Задаем произвольную точку P.
- Начинаем обходить все ребра многоугольника по часовой стрелке.
- На каждом шаге вычисляем угол между ребром и вектором, соединяющим начальную точку ребра с точкой P.
- При этом, если угол отрицателен, увеличиваем счетчик на 1, а если угол положителен, уменьшаем счетчик на 1.
- После обхода всех ребер многоугольника, счетчик должен быть равен 0 (если точка P лежит внутри многоугольника) или не равен 0 (если точка P лежит вне многоугольника).
Данный метод основан на том, что сумма углов, образованных вектором и ребром многоугольника, всегда равна 180 градусам. Если точка P находится внутри многоугольника, то сумма всех углов будет равна 360 градусам (+/- погрешность), что приведет к нулевому счетчику. Если же точка P находится вне многоугольника, то сумма углов будет меньше или больше 360 градусов, что приведет к ненулевому значению счетчика.
Этот метод обладает высокой эффективностью и простотой реализации. Он позволяет определять принадлежность точки многоугольнику в линейном времени, то есть с линейной сложностью относительно количества вершин многоугольника.
Применение этого метода может быть полезным при решении задач в компьютерной графике, например, при проверке пересечений объектов, определении области видимости или построении тени.
Эффективный способ определения принадлежности точки

Один из наиболее эффективных способов определения принадлежности точки многоугольнику основан на использовании алгоритма "трассировки лучей". Идея этого алгоритма заключается в следующем: мы проводим луч из рассматриваемой точки в любом направлении, и считаем количество пересечений этого луча с рёбрами многоугольника. Если это количество нечётное, то точка находится внутри многоугольника, иначе она находится снаружи.
Для реализации этого алгоритма необходимо представить многоугольник в виде последовательности его вершин и рёбер. При проведении луча из рассматриваемой точки, мы проверяем пересечение этого луча с каждым ребром многоугольника. Если пересечение происходит, то увеличиваем счётчик пересечений. После проверки всех рёбер, мы сравниваем значение счётчика с нулевым значением или с нечётным числом, чтобы определить принадлежность точки многоугольнику.
Алгоритм "трассировки лучей" обладает высокой эффективностью в сравнении с другими методами определения принадлежности точки многоугольнику, особенно при работе с большими многоугольниками и большим количеством точек.



